0. xCoba` at a glance

xCoba`  has been built on xTensor`  and shares its approach and priorities. In particular a great deal of effort has been made to allow full compatibility between abstract and component computations. A crucial ingredient has been the formalism of marked indices and particularly the treatment of frame dependent objects. Perhaps the most conspicuous example is the covariant parallel derivative, which follows the concept of ordinary derivative as described on Wald's General Relativity.  This reference has been the main inspiration for much of the notation, and the user is advised to keep it in mind when dealing with some of the non standard ideas employed by this package.

A session with xCoba` begins just like one with xTensor`, defining one or more manifolds and vector bundles and the objects living on them:

Define a 3d manifold M3:

In[10]:=

DefManifold[M3, 3, {a, b, c, d, e, f}]

** DefManifold: Defining manifold M3.

** DefVBundle: Defining vbundle TangentM3.

Define a complex vector bundle

In[11]:=

DefVBundle[InnerC, M3, 2, {A, B, C, D, F, G}, Dagger→Complex]

** DefVBundle: Defining vbundle InnerC.

ValidateSymbol :: capital : System name C is overloaded as an abstract index.

ValidateSymbol :: capital : System name D is overloaded as an abstract index.

** DefVBundle: Defining conjugated vbundle InnerC†. Assuming fixed anti-isomorphism between InnerC and InnerC†

Define a contravariant vector v and a covariant symmetric tensor T:

In[12]:=

DefTensor[v[a], M3]

DefTensor[T[-a, -b], M3, Antisymmetric[{-a, -b}]]

** DefTensor: Defining tensor v[a] .

** DefTensor: Defining tensor T[-a, -b] .

Define a Riemann symmetric tensor and a covariant vector on InnerC

In[14]:=

DefTensor[u[-A], M3, Dagger→Complex]

** DefTensor: Defining tensor u[-A] .

** DefTensor: Defining tensor u†[-A†] .

In[15]:=

DefTensor[R[-A, -B, -C, -D], M3, RiemannSymmetric[{1, 2, 3, 4}], Dagger→Complex]

** DefTensor: Defining tensor R[-A, -B, -C, -D] .

** DefTensor: Defining tensor R†[-A†, -B†, -C†, -D†] .

Remember that, in xTensor`, we use abstract indices

In[16]:=

T[-a, -b] v[b]

Out[16]=

T_ab^   v_ ^b

Now xCoba`  lets us define  bases. We have to specify its cnumbers (integers identifying the vectors of the basis) and vector bundle. Several related objects are also defined (parallel derivative and associated tensors).

In[17]:=

DefBasis[polar, TangentM3, {0, 1, 2}]

** DefCovD: Defining parallel derivative PDpolar[-a] .

** DefTensor: Defining torsion tensor TorsionPDpolar[a, -b, -c] .

** DefTensor: Defining non-symmetric Christoffel tensor ChristoffelPDpolar[a, -b, -c] .

** DefTensor: Defining vanishing Riemann tensor RiemannPDpolar[-a, -b, -c, d] .

** DefTensor: Defining vanishing Ricci tensor RicciPDpolar[-a, -b] .

** DefTensor: Defining antisymmetric +1 density etaUppolar[a, b, c] .

** DefTensor: Defining antisymmetric -1 density etaDownpolar[-a, -b, -c] .

Each basis has a colour, used to identify its associated objects in StandardForm

In[18]:=

DefBasis[cartesian, TangentM3, {0, 1, 2}, BasisColor→RGBColor[0, 0, 1]]

** DefCovD: Defining parallel derivative PDcartesian[-a] .

** DefTensor: Defining torsion tensor TorsionPDcartesian[a, -b, -c] .

** DefTensor: Defining non-symmetric Christoffel tensor ChristoffelPDcartesian[a, -b, -c] .

** DefTensor: Defining vanishing Riemann tensor RiemannPDcartesian[-a, -b, -c, d] .

** DefTensor: Defining vanishing Ricci tensor RicciPDcartesian[-a, -b] .

** DefTensor: Defining antisymmetric +1 density etaUpcartesian[a, b, c] .

** DefTensor: Defining antisymmetric -1 density etaDowncartesian[-a, -b, -c] .

We can define bases on the complex vector bundle. This generates additional objects for its parallel derivative (FRiemann and AChristoffel)

In[19]:=

DefBasis[complex, InnerC, {4, 5}, Dagger→Complex, BasisColor→RGBColor[0, 1, 0]]

** DefCovD: Defining parallel derivative PDcomplex[-a] .

** DefTensor: Defining torsion tensor TorsionPDcomplex[a, -b, -c] .

** DefTensor: Defining non-symmetric Christoffel tensor ChristoffelPDcomplex[a, -b, -c] .

** DefTensor: Defining vanishing Riemann tensor RiemannPDcomplex[-a, -b, -c, d] .

** DefTensor: Defining vanishing Ricci tensor RicciPDcomplex[-a, -b] .

** DefTensor: Defining nonsymmetric AChristoffel tensor  AChristoffelPDcomplex[A, -b, -C] .

** DefTensor: Defining nonsymmetric AChristoffel tensor  AChristoffelPDcomplex†[A†, -b, -C†] .

** DefTensor: Defining vanishing FRiemann tensor FRiemannPDcomplex[-a, -b, -C, D] .

** DefTensor: Defining vanishing FRiemann tensor FRiemannPDcomplex†[-a, -b, -C†, D†] .

** DefTensor: Defining antisymmetric +1 density etaUpcomplex[A, B] .

** DefTensor: Defining antisymmetric +1 density etaUpcomplex†[A†, B†] .

** DefTensor: Defining antisymmetric -1 density etaDowncomplex[-A, -B] .

** DefTensor: Defining antisymmetric -1 density etaDowncomplex†[-A†, -B†] .

As we advanced on the introduction, all the objects that depend on a particular basis are marked with its colour, for example here the parallel derivative of the basis

In[20]:=

PDpolar[-a][T[-b, -c]]

Out[20]=

_a^ T_bc^  

Now we can use basis indices and work with specific components. A contravariant basis index (BIndex) is represented by {a, basis}, where a is a valid abstract index and basis an existing basis. A covariant basis index is represented by {-a, -basis}.   If we give an integer instead of an abstract index we get a component index (CIndex):

In[21]:=

T[{-a, -polar}, b] v[{1, cartesian}]

Out[21]=

T_a ^( b) v_ ^1

Covariant component indices are represented by {i, -basis}, not by {-i, -basis}. This is because we consider the bases on the tangent and cotagent bundles to have the same cnumbers (and also allows us to use nonpositive  integers as cnumbers):

In[22]:=

v[{1, -cartesian}]

Out[22]=

v_1^

Basis vectors and transition matrices are represented by the two-index object Basis.

In[23]:=

Basis[A, {4, -complex}]

Out[23]=

e_ ( 4)^A

In[24]:=

Basis[{a, polar}, {-b, -cartesian}]

Out[24]=

e_ ( b)^a

Bases objects are not automatically contracted with one another:

In[25]:=

Basis[a, {-b, -polar}] Basis[-a, {c, cartesian}]

Out[25]=

e_a ^( c) e_ ( b)^a

In[26]:=

Basis[a, {1, -cartesian}] T[-a, -b]

Out[26]=

e_ ( 1)^a T_ab^  

We must use the function ContractBasis to force the operation.

In[27]:=

ContractBasis[%]

Out[27]=

T_ (1b)^  

This function is quite general and allows the user to specify which indices should be acted upon.The default is total contraction:

In[28]:=

expr = Basis[a, {1, -polar}] Basis[-c, {1, cartesian}] v[-a, -b, c, {d, polar}] Basis[{-d, -polar}, e]

Out[28]=

e_ ( 1)^a e_c ^( 1) e_ ( d)^e v_ab  ^(  cd)

In[29]:=

ContractBasis[expr]

Out[29]=

v_ (1b  )^(  1e)

In[30]:=

ContractBasis[expr, polar]

Out[30]=

e_ ( 1)^a e_c ^( 1) v_ab  ^(  ce)

In[31]:=

ContractBasis[expr, a]

Out[31]=

e_c ^( 1) e_ ( d)^e v_ (1b  )^(  cd)

The inverse function is SeparateBasis, also quite general. It can undo the action of ContractBasis and also change the basis of the whole expression

In[32]:=

cexpr = ContractBasis[expr]

Out[32]=

v_ (1b  )^(  1e)

In[33]:=

SeparateBasis[AIndex][cexpr]

Out[33]=

e_ (     1)^f$290 e_f$291 ^(     1) v_f$290b      ^(      f$291e)

In[34]:=

SeparateBasis[cartesian][cexpr]

Out[34]=

In[35]:=

%//ScreenDollarIndices

Out[35]=

e_b ^( c) e_ ( f)^e e_ ( d)^1 e_1 ^( a) v_ (ac  )^(  df)

One of the most important features of the package is the ability to trace basis contractions,

In[36]:=

TraceBasisDummy[v[{a, cartesian}] T[{-a, -cartesian}, -b]]

Out[36]=

T_ (0b)^   v_ ^0 + T_ (1b)^   v_ ^1 + T_ (2b)^   v_ ^2

We can produce lists of all the basis vectors,

In[37]:=

BasisArray[polar][a]

Out[37]=

{e_ ( 0)^a , e_ ( 1)^a , e_ ( 2)^a }

In[38]:=

BasisArray[polar, cartesian, cartesian][a, b, c]//MatrixForm

Out[38]//MatrixForm=

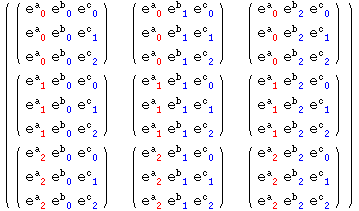
and lists of all the components of a tensor

In[39]:=

ComponentArray[T[{-a, -cartesian}, {-b, -cartesian}]]

Out[39]=

Notice that T is a symmetric tensor, so this can be simplified

In[40]:=

Simplification[%]//MatrixForm

Out[40]//MatrixForm=

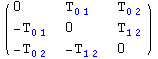
( {{0, T_ (01)^  , T_ (02)^  }, {-T_ (01)^  , 0, T_ (12)^  }, {-T_ (02)^  , -T_ (12)^  , 0}} )

We can assign rules to the components of a tensor taking the symmetries into account

In[41]:=

values = Table[i + j, {i, 3}, {j, 3}] ;

In[42]:=

AllComponentValues[T[{-a, -polar}, {-b, -polar}], values]

Added dependent rule T_ (00)^  →0 for tensor T

Added independent rule T_ (01)^  →3 for tensor T

Added independent rule T_ (02)^  →4 for tensor T

Added dependent rule T_ (10)^  → -T_ (01)^   for tensor T

Replaced independent rule T_ (01)^  →3 by T_ (01)^  → -3 for tensor T

Added dependent rule T_ (11)^  →0 for tensor T

Added independent rule T_ (12)^  →5 for tensor T

Added dependent rule T_ (20)^  → -T_ (02)^   for tensor T

Replaced independent rule T_ (02)^  →4 by T_ (02)^  → -4 for tensor T

Added dependent rule T_ (21)^  → -T_ (12)^   for tensor T

Replaced independent rule T_ (12)^  →5 by T_ (12)^  → -5 for tensor T

Added dependent rule T_ (22)^  →0 for tensor T

Out[42]=

In[43]:=

ColumnForm/@TensorValues[T]

Out[43]=

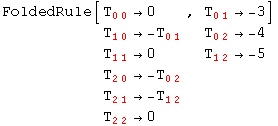
As we can see, dependent and independent components are stored in separate sublists. We can change basis:

In[44]:=

$CVVerbose = False ;

In[45]:=

ChangeComponents[T[-{a, cartesian}, -{b, cartesian}], T[-{a, polar}, -{b, polar}]]

Computed T_ (ab)^  →e_b ^( c) T_ (ac)^   in 0.050701 Seconds

Computed T_ (ab)^  →e_a ^( c) T_ (cb)^   in 0.134292 Seconds

Out[45]=

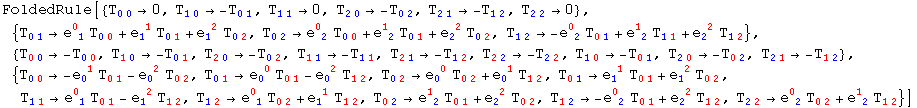
In[46]:=

ColumnForm/@TensorValues[T, {{-cartesian, -cartesian}}]

Out[46]=

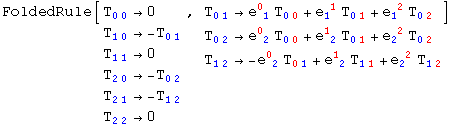
Clean up:

In[47]:=

DeleteTensorValues[T]

Deleted values for tensor T, derivatives {} and bases {{-cartesian, -cartesian}} .

Deleted values for tensor T, derivatives {} and bases {{-cartesian, -polar}, {-polar, -cartesian}} .

Deleted values for tensor T, derivatives {} and bases {{-polar, -polar}} .

In[48]:=

$CVVerbose = True ;

In[49]:=

Remove[expr, cexpr, values] ;

xCoba`  introduces new definitions to work with derivatives. Remember that each basis has an associated parallel derivative  (PDbasisname). We can express any derivative of a Basis object in terms of Christoffel tensors relating that derivative to the PD of the basis

In[50]:=

PDpolar[-a][Basis[{b, polar}, -c]]

Out[50]=

0

In[51]:=

PD[-a][Basis[{1, polar}, -c]]

Out[51]=

Γ[] _ ( ac)^1  

If we have a basis change a new Christoffel tensor is defined, relating the PDs of both bases

In[52]:=

PD[-a][Basis[{c, polar}, {-b, -cartesian}]]

** DefTensor: Defining tensor ChristoffelPDcartesianPDpolar[a, -b, -c] .

Out[52]=

-Γ[, ] _ ( ab)^c  

In[53]:=

PD[-a][Basis[{b, cartesian}, {2, -polar}]]

Out[53]=

Γ[, ] _ ( a2)^b  

We can define charts.

In[54]:=

DefChart[coord, M3, {0, 1, 2}, {x[], y[], z[]}]

** DefTensor: Defining tensor x[] .

** DefTensor: Defining tensor y[] .

** DefTensor: Defining tensor z[] .

** DefCovD: Defining parallel derivative PDcoord[-a] .

** DefTensor: Defining vanishing torsion tensor TorsionPDcoord[a, -b, -c] .

** DefTensor: Defining symmetric Christoffel tensor ChristoffelPDcoord[a, -b, -c] .

** DefTensor: Defining vanishing Riemann tensor RiemannPDcoord[-a, -b, -c, d] .

** DefTensor: Defining vanishing Ricci tensor RicciPDcoord[-a, -b] .

** DefTensor: Defining antisymmetric +1 density etaUpcoord[a, b, c] .

** DefTensor: Defining antisymmetric -1 density etaDowncoord[-a, -b, -c] .

Now the torsion tensor vanishes and the Christoffel is symmetric. Functions to restrict a field to a point or express it in terms of functions of the coordinates are currently under development.

In[55]:=

UndefBasis/@{polar, cartesian} ;

** UndefTensor: Undefined tensor ChristoffelPDcartesianPDpolar

** UndefTensor: Undefined non-symmetric Christoffel tensor ChristoffelPDpolar

** UndefTensor: Undefined vanishing Ricci tensor RicciPDpolar

** UndefTensor: Undefined vanishing Riemann tensor RiemannPDpolar

** UndefTensor: Undefined torsion tensor TorsionPDpolar

** UndefCovD: Undefined parallel derivative PDpolar

** UndefTensor: Undefined antisymmetric +1 density etaUppolar

** UndefTensor: Undefined antisymmetric -1 density etaDownpolar

** Undefined basis polar

** UndefTensor: Undefined non-symmetric Christoffel tensor ChristoffelPDcartesian

** UndefTensor: Undefined vanishing Ricci tensor RicciPDcartesian

** UndefTensor: Undefined vanishing Riemann tensor RiemannPDcartesian

** UndefTensor: Undefined torsion tensor TorsionPDcartesian

** UndefCovD: Undefined parallel derivative PDcartesian

** UndefTensor: Undefined antisymmetric +1 density etaUpcartesian

** UndefTensor: Undefined antisymmetric -1 density etaDowncartesian

** Undefined basis cartesian

Removing a complex basis also removes its complex conjugate:

In[56]:=

UndefBasis[complex] ;

** Undefined basis complex†

** UndefTensor: Undefined nonsymmetric AChristoffel tensor AChristoffelPDcomplex†

** UndefTensor: Undefined nonsymmetric AChristoffel tensor AChristoffelPDcomplex

** UndefTensor: Undefined non-symmetric Christoffel tensor ChristoffelPDcomplex

** UndefTensor: Undefined vanishing FRiemann tensor FRiemannPDcomplex†

** UndefTensor: Undefined vanishing FRiemann tensor FRiemannPDcomplex

** UndefTensor: Undefined vanishing Ricci tensor RicciPDcomplex

** UndefTensor: Undefined vanishing Riemann tensor RiemannPDcomplex

** UndefTensor: Undefined torsion tensor TorsionPDcomplex

** UndefCovD: Undefined parallel derivative PDcomplex

** UndefTensor: Undefined antisymmetric +1 density etaUpcomplex†

** UndefTensor: Undefined antisymmetric +1 density etaUpcomplex

** UndefTensor: Undefined antisymmetric -1 density etaDowncomplex†

** UndefTensor: Undefined antisymmetric -1 density etaDowncomplex

** Undefined basis complex

In[57]:=

UndefChart[coord]

** UndefTensor: Undefined tensor x

** UndefTensor: Undefined tensor y

** UndefTensor: Undefined tensor z

** UndefTensor: Undefined symmetric Christoffel tensor ChristoffelPDcoord

** UndefTensor: Undefined vanishing Ricci tensor RicciPDcoord

** UndefTensor: Undefined vanishing Riemann tensor RiemannPDcoord

** UndefTensor: Undefined vanishing torsion tensor TorsionPDcoord

** UndefCovD: Undefined parallel derivative PDcoord

** UndefTensor: Undefined antisymmetric +1 density etaUpcoord

** UndefTensor: Undefined antisymmetric -1 density etaDowncoord

Created by Mathematica  (May 16, 2008) Valid XHTML 1.1!