xCobaDoc.nb_23.html

7. Assigning values to components

We need some convenient way to store all the values of the components of a tensor (or, more generally, an arbitrary expression). xCoba` provides several tools to accomplish this, optimised to make full use of the symmetries. This section describes how to store and use these values, but not how to compute them. The latter is the object of Section 9 (not yet fully implemented).

Given a tensor there are several things we need to worry about when working with values:
    - 1. Are we giving values to the components of the tensor itself or to some derivative of it?
    - 2. The slot-symmetry of the expression.
    - 3. What is the character of the c-indices involved?
    - 4. Which bases are we using to form the component?
    - 5. When did we construct a particular set of components?
    - 6. Have we already computed values for all components of the expression?

This section describes a series of functions for the storage of tensor values. After reading it, we think it is very profitable to take a look at the notebook Schwarzschild.nb, by Alfonso García-Parrado, which describes an example computation with the Schwarzschild metric, employing some of the commands described here. This notebook is included in xCoba.tar.gz and can be downloaded from http://metric.iem.csic.es/Martin-Garcia/xAct/index.html.

7.1. FoldedRule and ValID

7.2. ComponentValue and TensorValues without independent values

ComponentValue        Give the value of a single component
TensorValues        List of all values for a given tensor
TensorValIDs        List of all the ValIDs of a given tensor
DateOfValID            Time a given ValID was generated
$CVVerbose            Switch verbose output on/off for ComponentValue

Storing values for components

We have seen how xCoba` stores and labels sets of tensor values for different basis configurations; this section describes how these sets are generated. The basic function is ComponentValue, which generates the rule for a single component. ComponentValue can be called with one or two arguments:

In[314]:=

We begin by examining how it works with just one argument (i.e. without specifying an independent value). Let us define a totally antisymmetric tensor

In[315]:=

In[316]:=

Out[316]=

Suppose we want to generate a rule for one of its components

In[317]:=

Out[317]=

In[318]:=

Out[318]=

In[319]:=

Out[319]=

$FoldedRule[{}, {W_ ^(012) →W_ ^(012)}]$

As we can see, xCoba` has recognised that is an independent component and has added a rule for it in the second list of the FoldedRule. This rule is trivial, as we have not specified the numerical value of the component. But consider now the following

In[320]:=

Out[320]=

In[321]:=

Out[321]=

$FoldedRule[{W_ ^(210) → -W_ ^(012)}, {W_ ^(012) →W_ ^(012)}]$

xCoba` sees that is not an independent component and generates for it a rule in the first list of the FoldedRule. We can easily generate the full set of component values:

In[322]:=

Out[322]=

In[323]:=

Out[323]=

As we can see by reading the messages, the rules for and have not been recomputed. Now

In[324]:=

Out[324]=

There is only one independent rule. We have one ValID for , which consists of only one basis configuration

In[325]:=

Out[325]=

ValIDs are timestamped:

In[326]:=

Out[326]=

Let us now consider an example with several bases. Recall that is a symmetric tensor

In[327]:=

Out[327]=

In[328]:=

Out[328]=

In[329]:=

Out[329]=

In[330]:=

Out[330]=

We still do not have all the rules, because our ValID mixes the cases and :

In[331]:=

Out[331]=

In[332]:=

Out[332]=

In[333]:=

Out[333]=

In[334]:=

Out[334]=

Now we still only have one ValID for , but it consists of two basis configurations. As we can see, the FoldedRule returned by TensorValues mixes the cases and . Another example, now mixing index characters:

In[335]:=

Out[335]=

${T_ ( 0)^0 , T_ ( 1)^0 , T_ ( 2)^0 , T_ ( 0)^1 , T_ ( 1)^1 , T_ ( 2)^1 , T_ ( 0)^2 , T_ ( 1)^2 , T_ ( 2)^2 }$

In[336]:=

Out[336]=

In[337]:=

Out[337]=

${T_0 ^( 0), T_0 ^( 1), T_0 ^( 2), T_1 ^( 0), T_1 ^( 1), T_1 ^( 2), T_2 ^( 0), T_2 ^( 1), T_2 ^( 2)}$

In[338]:=

Out[338]=

In[339]:=

Out[339]=

We have two ValIDs, both consisting of two basis configurations. Notice how newer ValIDs appear first.We can retrieve the TensorValues for either one of them

In[340]:=

Out[340]=

or for all at the same time:

In[341]:=

Out[341]=

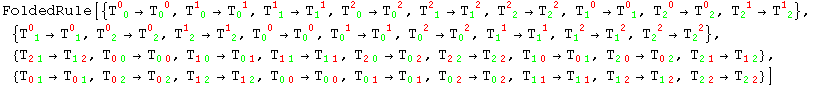
We can delete single rules

In[342]:=

Out[342]=

We can also easily delete all TensorValues for a given tensor

In[343]:=

or only those for a single ValID

In[344]:=

7.3. ComponentValue and TensorValues with independent values

7.4. AllComponentValues

7.5. Components and derivatives

7.6. BasisValues

7.7. Components of the metric, MetricInBasis

7.7. Changing bases or index characters

ChangeComponents Compute new TensorValues from an already stored index configuration

Changing bases or index characters

Suppose we already have the tensor values for a given ValID and we want to generate the corresponding set for an (inequivalent) index configuration. We may want to perform a typical change of basis like to , for example. Or we may want to lower or raise some indices. Given starting and finishing index configurations, xCoba` can compute the best route between them with the function ChangeComponents

A simple example

In[380]:=

Out[380]=

In[381]:=

Out[381]=

In[382]:=

A more complicated example, with an antisymmetric tensor . To keep it shorter we can change the cnumbers of polar to make xCoba` think the manifold is two dimensional

In[383]:=

In[384]:=

$CNumbersOf[polar] ^={1, 2}$

Out[384]=

We set some configuration global variables

In[385]:=

In[389]:=

Out[389]=

The system prints Value + expected to be 0 by symmetry.This is because of $UseValues =ToCanonical which tells the system only to use the independent rules at each step. If we had written $UseValues =All instead that message would not have appeared. However, whenever a component is 0 because of the symmetry, the symmetry value is used, so our result is correct.