7.1. FoldedRule and ValID
FoldedRule List of lists of rules to be applied sequentially
ValID Identifier for each independent set of components stored for a tensor
TensorValIDs List of all the ValIDs of a given tensor
DateOfValID Time a given ValID was generated
Identifying sets of component values
Before introducing the general functions, let us consider a simple example. Let us suppose we have a rank two tensor 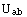 , with no symmetries and only one basis. Then, the straightforward way of storing its components would be with a list of replacement rules:
, with no symmetries and only one basis. Then, the straightforward way of storing its components would be with a list of replacement rules:
{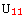 → a,
→ a, 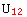 → b,
→ b, 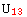 → c, ...}
→ c, ...}
But now consider, still with just one basis in play and no metric, that our tensor 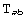 is symmetric. Then it would be a waste to store twice the component
is symmetric. Then it would be a waste to store twice the component 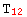 =
=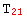 , for example. With higher rank tensors and higher symmetries the redundancy makes the process very inefficient. Instead, we could think of storing components as a pair of lists. The first one would give the relations due to symmetry and the second one the values of the independent components. We could have something like
, for example. With higher rank tensors and higher symmetries the redundancy makes the process very inefficient. Instead, we could think of storing components as a pair of lists. The first one would give the relations due to symmetry and the second one the values of the independent components. We could have something like
{ {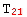 →
→ 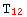 ,
, 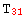 →
→ 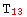 ,
, 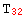 →
→ 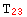 }, {
}, { 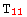 → a,
→ a, 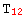 → b,
→ b, 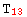 → c,
→ c, 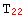 → d,
→ d, 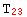 → e,
→ e, 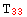 → f} }
→ f} }
It may appear we have gained nothing, after all we still have 9 rules. However, all the information of the first list is determined by the symmetry group of the tensor, which xCoba` already knows since its definition. Also, the independent values may be very large expressions while the dependent rules are always very simple. This structure is represented in xCoba` with the concept of FoldedRule (defined in the auxiliary package xCore`):
In[311]:=
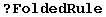
![FoldedRule[rules1, rules2, ...] contains a number of lists of rules which are applied sequentially (first rules1, then rules2, etc.) when called by ReplaceAll and ReplaceRepeated.](../HTMLFiles/xCobaDoc.nb_856.gif)
Example:
In[312]:=
![x + t/.FoldedRule[{x→y, t→x}, {y→z}]](../HTMLFiles/xCobaDoc.nb_857.gif)
Out[312]=
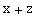
In the next subsection we shall see how xCoba` generates these lists. The next problem comes when we consider a more general case where we have a metric and several bases. In this situation we may want to store the values for a given tensor in different bases and with different index characters. However, not all those combinations are independent. Recalling our symmetric tensor 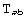 , we see that the FoldedRules that would contain its values for
, we see that the FoldedRules that would contain its values for 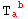 and
and 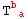 would have the same independent components (likewise for
would have the same independent components (likewise for 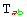 and
and 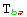 ). So among all sets of values for a tensor, only some will be independent. xCoba` identifies these independent sets with the concept of ValID:
). So among all sets of values for a tensor, only some will be independent. xCoba` identifies these independent sets with the concept of ValID:
In[313]:=
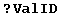

Continuing with our example, we would have for our tensor 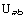 a single ValID, which would be
a single ValID, which would be
ValID[U, { {polar, polar}} ]
(both indices in the base polar). We have several for 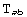
ValID[T, { {polar, -polar} , {-polar, polar}} ]
ValID[T, { {polar, cartesian}, {cartesian, polar}]
The first would represent the fact that 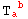 and
and 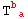 have the same independent rules and the second would represent the situation for
have the same independent rules and the second would represent the situation for 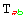 and
and 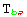 . Notice how even in the case of
. Notice how even in the case of 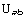 , where there is only one possible basis configuration in the ValID, we give a list of lists of bases. The command VTensorValIDs returns all the ValIDs we have stored for a given tensors (and its derivatives, as we shall see below).
, where there is only one possible basis configuration in the ValID, we give a list of lists of bases. The command VTensorValIDs returns all the ValIDs we have stored for a given tensors (and its derivatives, as we shall see below).
All of this will be much clearer once we see how xCoba` generates the FoldedRules and their corresponding ValIDs for a tensor in the next subsection.
