The integrand of the Wald entropy formula,
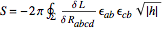
can be computed by varying a Lagrangian
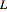
w.r.t. to the Riemann tensor. But because derived curvature tensors such as the Ricci and Weyl tensors don't explicitly depend on the Riemann tensor in xAct, we must convert them to Riemann tensors.
Let us take the square of the Weyl tensor as the Lagrangian:
And define a antisymmetric tensor for the binormal to the black hole horizon:
Convert the Lagrangian to Riemann tensors (note that curvature relations must be disabled for this to work, see
ClearCurvatureRelations):
This can then be varied w.r.t. to the Riemann tensor by using
VarD to obtain the integrand of the entropy:
Note that whenever your Lagrangian has covariant derivatives, you must first
symmetrized them before taking the variation w.r.t. to the Riemann in order to get correct results for the entropy.