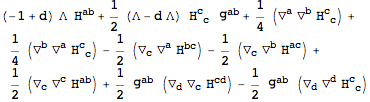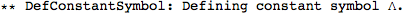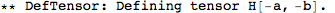AdS Perturbations
xTras has a number of functions that allow for perturbations around (A)dS backgrounds. Before discussing them, we'll first have a look at the basic functionality provided in the native
xAct package
xPert.
xPert functions
| Perturbation[expr,n] | returns the nth order perturbation of expr |
| ExpandPerturbation[expr] | expand any unexpanded Perturbation[tensor] terms in expr |
| DefTensorPerturbation[pert,tens,M] | defines the perturbation pert for the tensor tens on the manifold M |
| DeMetricPerturbation[g,pert,par] | defines the perturbation pert of the metric g and the perturbations of the associated curvature tensors, with expansion parameter par |
Main xPert functions.
Expression can be perturbed with
Perturbation:
| Out[11]= | 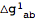 |
| Out[12]= | 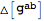 |
| Out[10]= | 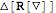 |
This gives the unexpanded perturbations of the input expressions, unless the input is a tensor for which a perturbation is defined.
xTras automatically defines a metric perturbation (see the tutorial
Metric Variations), hence the perturbation of the metric returned the perturbation tensor
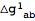
.
The unexanded perturbations can be expanded with
ExpandPerturbation:
| Out[13]= | 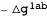 |
| Out[14]= | 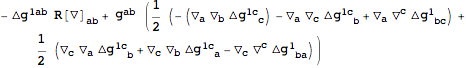 |
This expanded the expressions in terms of any defined tensor perturbations, in this case
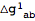
. The covariant derivatives and the curvature tensors are now those of the background. They can easily be replaced with particular background values with the help of
xTras functions.
xTras additions
We'll now turn the xTras functions tailor-made for doing perturbations around (A)dS backgrounds.
| SymmetricSpaceRules[cd,K] | produces replacement rules for the curvature tensors of the covariant derivative cd on a symmetric space of constant curvature K |
| ToBackground[expr] | sends unperturbed (curvature) tensors to background values |
| ExpandBackground[expr] | returns the perbutation expansion of expr on an arbitrary background |
The main functions for doing AdS perturbations.
Setting up
In this section we will set up things to do perturbations around AdS. First, begin with defining a constant symbol for the cosmological constant.
Next, compute the equations of motion for the Einstein-Hilbert term plus a cosmological constant with
VarL.
| Out[45]= | 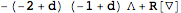 |
| Out[46]= | 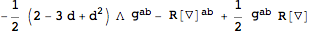 |
Now make rules for the background solution of these equations of motion with
SymmetricSpaceRules:
| Out[33]= |  |
Check that the background actually solves the equations of motion:
| Out[44]= | 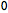 |
We now set this background to the default background solution of
ToBackground. It then also becomes the default background for
PerturbBackground and
ExpandBackground.
Checking that the background solves the equations of motion can now be done with
ToBackground:
| Out[50]= | 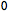 |
Linearizing the equations of motion
We can now expand the equations of motion on this background with
ExpandBackground, in order to obtain the linearized Einstein equations:
| Out[54]= | 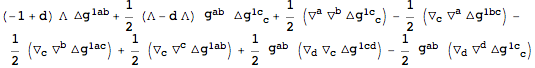 |
The tensor
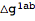
has a first index that labels the perturbation order. Often, it is convenient to remove this label. To that end, we define a new tensor that we will use as the metric perturbation.
We can now replace
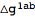
with this new tensor:
| Out[57]= | 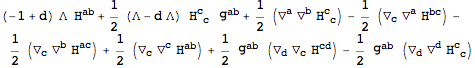 |
This process of replacing
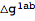
with
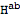
can be automated by setting another option of ToBackground. The second rule below is for eliminating all higher order perturbations.
Expanding on the background now automatically replaces
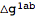
with
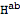
:
| Out[59]= | 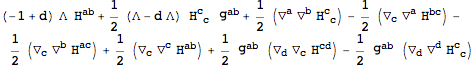 |
Linearizing the action
Instead of perturbing the equations of motion, we can also perturb the action. Of course, the first non-trivial order here is not the first, but the second.
| Out[61]= | 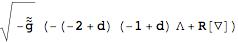 |
| Out[66]= |  |
When we vary the linear action with respect to
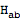
, we should obtain the linearized equations of motion:
| Out[67]= | 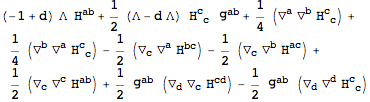 |
The difference between the two equations of motion is zero:
| Out[68]= | 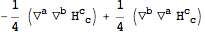 |
| Out[69]= | 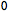 |
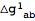 .
.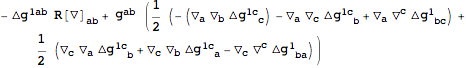
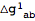 . The covariant derivatives and the curvature tensors are now those of the background. They can easily be replaced with particular background values with the help of xTras functions.
. The covariant derivatives and the curvature tensors are now those of the background. They can easily be replaced with particular background values with the help of xTras functions.
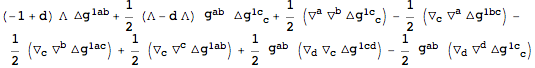
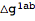 has a first index that labels the perturbation order. Often, it is convenient to remove this label. To that end, we define a new tensor that we will use as the metric perturbation.
has a first index that labels the perturbation order. Often, it is convenient to remove this label. To that end, we define a new tensor that we will use as the metric perturbation.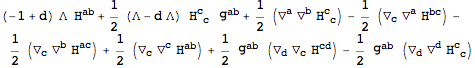
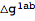 with
with 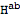 can be automated by setting another option of ToBackground. The second rule below is for eliminating all higher order perturbations.
can be automated by setting another option of ToBackground. The second rule below is for eliminating all higher order perturbations.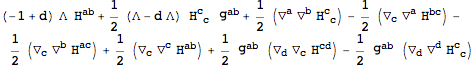

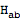 , we should obtain the linearized equations of motion:
, we should obtain the linearized equations of motion: