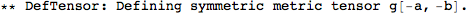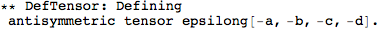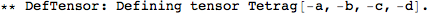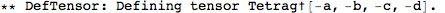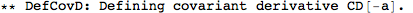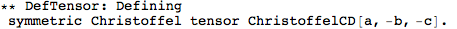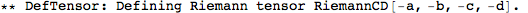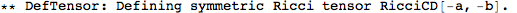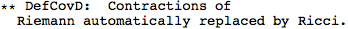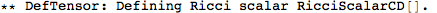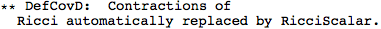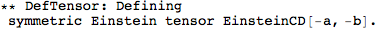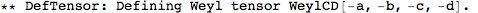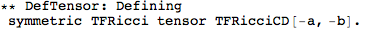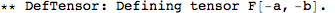| xTras Tutorial | |Functions » |
Introduction to xAct
xAct is a suite of free packages for tensor computer algebra in Mathematica. xAct implements state-of-the-art algorithms for fast manipulations of indices and has been modelled on the current geometric approach to General Relativity. It is highly programmable and configurable. Since its first public release in March 2004, xAct has been intensively tested and has solved a number of hard problems in GR.
| xCore | generic programming tools |
| xPerm | manipulation of large groups of permutations |
| xTensor | abstract tensor computations |
| xCoba | component tensor computations |
| xPert | high-order perturbation theory in GR |
| Harmonics | tensor spherical harmonics |
| Invar | polynomial invariants of the Riemann tensor |
| Spinors | spinor computations in GR |
| xPrint | formatted input |
| SymManipulator | symmetrized expressions |
| xTras | field theory inspired additions |
| TexAct | |
| xPand | cosmological perturbation theory |
| xTerior | differential forms |
Setting up a session
Let's start by getting a simple xAct session up and running, and define a manifold and tensors on that manifold.
| DefManifold[M,dim,inds] | defines a manifold M with dimension dim and a tangent bundle with indices inds. |
| DefMetric[sign,g[-a,-b],cd] | defines a metric g of signature sign on the manifold of which a and b are indices, a covariant derivative cd, and all curvature tensors of g. |
| DefTensor[T[inds],M,sym] | defines a tensor T with indices inds and symmetry sym on the manifold M. |
Commands for defining manifolds, metrics, and tensors.
This loaded not only the xTensor package, but also the xPerm package which handles the group theoretical computations needed for canonicalizing tensors.
Let's define a four-dimensiona manifold:
Let's define a four-dimensiona manifold:
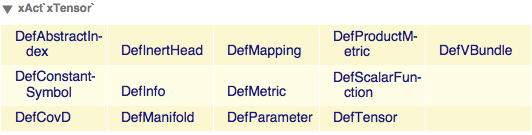
You'll notice that besides defining a manifold, this also defined a vector bundle TangentM where our tensors will live. In fact, xAct is build around the notion of 'defining' geometric quantities and tensors, and has quite some commands to do so. We can get a list of them with the Information command:
The two most important ones (next to DefManifold) are DefMetric, which defines the metric, and DefTensor, which defines a tensor. Let's first define a metric on our manifold M.
We don't need to specify the manifold, because xTensor determines that from the indices of the metric. But we do need to specify a symbol for the associated covariant derivative. We'll name it CD, and we'll let the metric be Lorentzian (hence the -1). The option CurvatureRelations is to ensure that contractions of Riemann tensors are automatically converted to Ricci's.
We don't need to specify the manifold, because xTensor determines that from the indices of the metric. But we do need to specify a symbol for the associated covariant derivative. We'll name it CD, and we'll let the metric be Lorentzian (hence the -1). The option CurvatureRelations is to ensure that contractions of Riemann tensors are automatically converted to Ricci's.
This did a whole lot of things. It first defined a metric, and then a number of curvature tensors (the Christoffel tensors, Riemann, Ricci's, the Weyl tensor, etc).
For instance, we now have a Riemann tensor. It has the same structure as every tensor in xAct, namely the name of the tensor followed by its indices. Because we named our covariant derivative CD, this Riemann tensor is called RiemannCD (it's the Riemann tensor of the covariant derivative CD). We can enter it as follows:
For instance, we now have a Riemann tensor. It has the same structure as every tensor in xAct, namely the name of the tensor followed by its indices. Because we named our covariant derivative CD, this Riemann tensor is called RiemannCD (it's the Riemann tensor of the covariant derivative CD). We can enter it as follows:
| In[4]:= |
| Out[4]= |
Note that it prints much nicer than how it's put in: xAct formats the indices properly and shortens the name of the tensor to something readable. But underneath it still has the same structure:
| In[5]:= |
Out[5]//InputForm= | |
The minus signs in front of the indices indicate that they're (covariant) lower indices. If we want to put in (contravariant) upper indices, we just forgo the minus sign:
| In[6]:= |
| Out[6]= |
is a valid xAct expression, even though it doesn't print its indices.
More complicated tensors can be defined by just specifying their index structure. We can also specify if it's (anti)symmetric as follows:
More complicated tensors can be defined by just specifying their index structure. We can also specify if it's (anti)symmetric as follows:
xAct does not automatically enforce the symmetries of the tensor. For instance, this should be zero:
| In[9]:= |
| Out[9]= |
Canonicalizing and contracting indices
| ToCanonical[expr] | gives a canonical reorganization of the indices of expr according to the symmetries of tensors and positions of dummies and repeated indices |
| ContractMetric[expr] | contracts all metrics in expr |
Arguably two of the most important functions in xAct.
ToCanonical canonicalizes expressions, which roughly means 'sorting the indices and introduce minus signs where necessary':
This didn't do anything, because the expression was already canonical (it's indices were already sorted).
The symmetrization of F does reduce to zero if we use ToCanonical:
The symmetrization of F does reduce to zero if we use ToCanonical:
ToCanonical also works on more general expressions and symmetries. Here is its action on a permutation of the Riemann tensor:
| In[18]:= |
| Out[18]= |
This is not automatically contracted. We have to use the function ContractMetric if we want to do so:
| In[10]:= |
Out[10]//InputForm= | |